Wer hat nicht gerne ein paar Steigungsstrecken auf seine Modelleisenbahn, um Dampfloks mit schweren Zügen den Berg hinauf schnaufen zu sehen? Wer benötigt eine Steigung, um eine Streckenkreuzung nicht niveaugleich installieren zu müssen? Gleichgültig, ob man will oder muss, die Fahrt bergauf und bergab erfordert beim Bau von Modelleisenbahn-Steigungen einige Überlegungen, die vielleicht umfangreicher sind, als man es erwartet.

Der Grund dafür ist, dass es hier um Geometrie und Physik geht. Gerade, weil das nicht jedermanns Sache ist, möchte ich versuchen, das Thema so verständlich wie möglich zu erklären. Um alles etwas übersichtlicher zu machen, teile ich die Materie in vier Teile auf:
- Unterschiedliche Definitionen von Modelleisenbahn-Steigungen
- Mögliche Steigungen einer Modelleisenbahn
- Steigungen und Kurvenradien
- Das Gleiswendel-Problem
Unterschiedliche Definitionen von Modelleisenbahn-Steigungen
Die Überschrift ist vielleicht etwas irritierend, aber wie beschreibt man eigentlich eine Steigung? Natürlich, es ist (in unserem Fall) eine Eisenbahn-Strecke, die an einem niedrigen Punkt beginnt und an einem höheren Punkt endet. Ein Gefälle ist genau das Gegenteil. Wie stark oder wie steil eine Steigung ist, das wird jedoch sehr unterschiedlich beschrieben. Sicher kennt jeder das Verkehrszeichen am Straßenrand, das eine Steigung oder ein Gefälle kennzeichnet. Da steht dann beispielsweise 5% oder 12% bei sehr steilen Straßen. Dabei bedeutet 1% oder 10‰, dass die Strecke um einen Meter pro 100 Meter ansteigt oder abfällt. Ein Prozent entspricht also zehn Promille.
Die Möglichkeit, die Stärke einer Steigung in Prozent (%) oder Promille (‰) anzugeben, ist allerdings nicht die einzige. Auch die Angabe des Winkels, den die Strecke von der horizontalen abweicht, kann eine Steigung oder ein Gefälle definieren. Eine dritte Methode beschreibt das Verhältnis der Strecke zum Höhenunterschied dieser Strecke vom Anfang zum Ende. Auch diese Methode wird bei Eisenbahnern im Original und im Modell verwendet.
Dann wollen wir die drei Systeme mal vergleichen!
Promille und Prozent
Nehmen wir an, unsere Steigungsstrecke auf der Modelleisenbahn hat eine Länge von 3 Metern und der Höhenunterschied vom Beginn der Strecke bis zum Ende beträgt 10 cm. Wir müssen aber mit einheitlichen Maßen messen, 3 Meter sind also 300 cm und 10 cm bleiben unverändert.
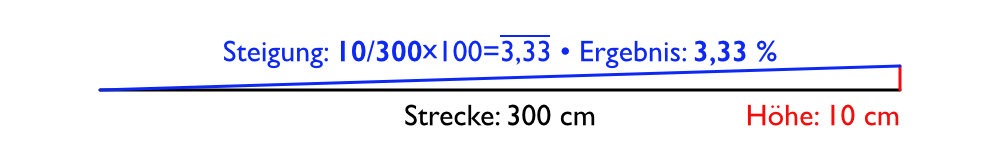
Prozent bedeutet 1 Teil von 100, bei 300 ist ein Teil also 3. Da wir eine Steigung von 10 cm haben und ein Teil 3 cm beträgt, teilen wir 10 cm durch 3. Das Ergebnis ist 3,33. Unsere Steigung beträgt also 3,33%. Das ist eine Steigung, die in der Realität schon eine Herausforderung darstellt und auch bei uns im Modell nicht von jedem Zug und jeder Lok bewältigt werden wird. Messwagen, wie der Märklin-Insider Waggon mit der Bestellnummer 46582 zeigen diesen Wert direkt an.
Winkel-Grade
Das Umrechnen von Streckenlängen und Höhenunterschieden in Winkelgraden ist dagegen etwas schwieriger. Ich bin sicher, nicht jeder erinnert sich gern an die Stunden zur Trigonometrie im Mathe-Unterricht seiner Schulzeit. Wer noch ein Geodreieck hat, kann die Steigung einer Strecke in Winkel-Graden (zumindest ungefähr) damit ermitteln.

Die Formel dazu lautet folgendermaßen:
Höhe / Strecke = tanα=Winkel
Um tanα (Tangens vom Winkel Alpha) in den tatsächlichen Winkel in Grad umzurechnen, benötigen wir einen Taschenrechner oder eine Taschenrechner-App auf dem Handy mit wissenschaftlichen Funktionen. Der berechnete Wert ist aber häufiger für Architekten und Landschaftsplaner interessant. Im Modellbau wird er eher selten eingesetzt. Viel wichtiger ist dagegen das folgende System, das sowohl in der Modellbahn, als auch im Vorbild, der großen Bahn eingesetzt wird.
Verhältnis der Strecke zum Höhenunterschied
Im Vergleich zu den obigen Methoden ist es sehr einfach, das Verhältnis der Strecke zum Höhenunterschied zu ermitteln. Dazu benötigt man die Länge der Steigungsstrecke und deren Höhenunterschied. Es können Meter, Kilometer oder Millimeter sein, das ist egal. Es müssen aber immer die gleichen Maßeinheiten gegenüber gestellt werden. Bei unserer Beispielstrecke beträgt die Länge 300 cm und der Höhenunterschied 10 cm. Um das Ergebnis zu erhalten, teilen wir die Strecke durch den Höhenunterschied. Das Ergebnis ist 30, unsere Steigung ist demzufolge 30 zu 1. Das bedeutet, dass wir 30 cm Strecke benötigen, um 1 cm Höhenunterschied zu erreichen.

Damit wird klar, dass wir mit allen drei Methoden arbeiten und zu den gleichen Ergebnissen in der Praxis kommen werden. Welche Steigungen in der Praxis der Modelleisenbahn und dem großen Vorbild aber realisierbar sind, damit beschäftigen wir uns im folgenden Absatz.
Mögliche Modelleisenbahn-Steigungen einer Anlage
Leider kann man die Steigung einer Modelleisenbahn-Strecke nicht beliebig steil gestalten. Das ist ja auch bei unserem großen Vorbild der Fall. Je steiler die Steigung einer Strecke ausfällt, um so größer ist die Gefahr, dass die Räder der Lokomotive durchdrehen oder schlimmer noch, die Lok am Berg nicht mehr anfahren kann und mit schleudernden Rädern auf der Stelle stehen bleibt. Die nötige Folge ist das Kürzen der Züge oder der Einsatz einer Doppel- oder sogar Dreifachtraktion, also von zwei Lokomotiven oder mehr an einem Zug.
Wer das vermeiden will, sollte die Steigungen wie beim Vorbild sehr moderat gestalten. Die oben genannten 3,33% sind dabei schon ein sehr extremer Wert. Üblicher sind Steigungen zwischen 1,5% und 2,0%.
Eine Ausnahme davon bildet dabei beispielsweise die legendäre Eisenbahnstrecke durch das Höllental im Schwarzwald, das mit Steigungen von bis zu 5,7% die Lokomotiven und die Lokführer vor echte Herausforderungen stellte. In Dampflokzeiten wurde diese Strecke meist mit zwei Lokomotiven pro Zug befahren. Die sehr schwere BR85 war dort regelmäßig vor Güterzügen im Einsatz. Heute befahren kurze RE-Züge mit einer E-Lok diese Strecke.
Auf der Modelleisenbahn hängt die mögliche Steigung von verschiedenen Faktoren ab. Die Anzahl der angetriebenen Achsen der Lokomotiven, die auf der Strecke verwendet werden sollen, spielt ebenso eine Rolle wie die Anzahl der Achsen, die bei diesen Lokomotiven mit Haftreifen ausgestattet sind. Das Gewicht der auf den Strecken eingesetzten Lokomotiven bestimmt ausserdem die möglichen zu befahrenden Steigungen. Zu guter Letzt bestimmt das Gewicht der zu ziehenden Waggons die zu befahrenden Modelleisenbahn-Steigungen. Es ist sicher einleuchtend, dass die ziehende Lokomotive auf Steigungsstrecken um so mehr belastet wird, je mehr Personen- oder Güterwagen der zu ziehende Zug enthält.
NEM 302
Natürlich ist alles genormt, auch das Gewicht eines Waggons auf der Modelleisenbahn. Laut NEM-Norm 302 (2015) soll das Gewicht eines Waggons (Wagenmasse) mindestens 0,4 g pro Millimeter Wagenlänge betragen. Diese Mindestmasse kann laut NEM 302 um bis zu 30%, also auf 0,54 g pro Millimeter Wagenlänge für eine erhöhte Wagenmasse gesteigert werden.
Erfahrene Modelleisenbahner sind daher zu folgenden Regeln gekommen, um die mögliche Zuglänge bei verschiedenen Steigungen zu bestimmen:
1zu20, 5%, 2,86º: ca. 5 Personenwagen oder 10 Güterwagen (für sehr kleine Anlagen)
1zu30, 3,33%, 1,9º: ca. 8 Personenwagen oder 16 Güterwagen (für kleine bis mittlere Anlagen)
1zu50, 2%, 1,15º: ca. 10 Personenwagen oder 20 Güterwagen (für große Anlagen)
1zu70, 1,4%, 0,82º: ca. 12 Personenwagen oder 35 Güterwagen (für sehr große Anlagen)
Die Folge dieser Erkenntnis wird sein, dass man wie immer zu wenig Platz auf seiner Modellbahnanlage hat. Das bringt uns zum dritten Kapitel dieses Textes. Man könnte doch die Steigungen auch in Kurvenform verlegen und würde viel Platz sparen. Wie so oft, hat leider auch diese Idee ihre Kehrseite …
Steigungen und Kurvenradien
Die Physik spielt uns leider einen üblen Streich, wenn die Steigungen einer Modelleisenbahn-Strecke nicht geradlinig verläuft, sondern in einer Kurve stattfindet. Die zusätzlich entstehende Reibung der Spurkränze an den Schienen sowie die unterschiedlichen Streckenlängen der Innen- und Aussenschienen einer Kurve und daraus resultierenden unterschiedlichen Reibungen der Räder an den Innen- und Aussenschienen bremst den Zug zusätzlich zur vorhandenen Steigung. Die scheinbare Steigung für die Lokomotive wird um so größer, je enger der zu befahrende Radius der Strecke ist.
Der amerikanische Modelleisenbahn-Guru John Allen hat dazu eine Faustregel aufgestellt, mit der sich ermitteln läßt, wie stark eine Kurve die Lokomotive zusätzlich bei einer Steigung belastet. Hier ist die auf europäische Verhältnisse übertragene Formel:
82 / Radius (cm) = Steigungszugabe (%)
Das bedeutet, wenn wir eine reale Steigung von 2,5% haben und diese in einer Kurve mit einem Radius von 40 cm verläuft, erhöht sich die scheinbare Steigung für die Lok auf 82 / 40 cm = 2,05% + 2,5% reale Steigung = 4,55%. Das ist wesentlich mehr, als in der Praxis problemlos möglich ist, es wird eine Steigung mit vielen Problemen im Alltag werden, insbesondere bei längeren Zügen. Die Lösung ist eine flachere reale Steigung und damit eine längere Steigungsstrecke oder ein deutlich größerer Radius der Kurve in der Steigung. Beides benötigt mehr Platz. Da haben wir es also wieder, unser ständiges Problem mit nicht ausreichendem Platz auf der Modelleisenbahn-Anlage,
Die Lösung ist aber eigentlich ganz einfach: man macht es wie Gerrit und Frederik Braun in Hamburg und mietet ein altes Lagerhaus oder eine ähnlich große Immobilie und baut ein Miniatur Wunderland mit einer Streckenlänge von rund 16.500 Metern. Da sind Radien und Steigungen dann wirklich kein Problem mehr!

(Foto: Karl H. Warkentin, mit freundlicher Genehmigung des Miniaturwunderland Hamburg)
Das Gleiswendel-Problem
Wollen wir also eine maximale effektive Steigung für einen Gleiswendel von beispielsweise 3% nicht überschreiten, dann bestimmt der gewünschte Höhenunterschied eines 360º Wendels den notwendigen Radius. Wir gehen mal davon aus, dass der Höhenunterschied von einer Ebene zur nächsten von Schienenoberkante zu Schienenoberkante 10 cm betragen soll. Bei einer Steigung von 3% muss also die Steigungsstrecke und damit der Umfang des Wendels in Schienenmitte 333,3 cm betragen. Zu diesem Wert gelangt man durch:
Höhenunterschied (cm) / Steigung (%) x 100 = Streckenlänge (cm)
Bei welchem Radius bekommen wir aber eine Streckenlänge von 333,3 cm bei einem Vollkreis von 360º? Dazu muss wieder ein bisschen Geometrie und die Kreiszahl π (ca. 3,14) helfen:
Streckenlänge (cm) / 3,14 = Durchmesser (cm) / 2 = Radius (cm)
Wir können die beiden Formeln oben zusammenfassen und erhalten:
Höhenunterschied (cm) / Steigung (%) x 100 / 3,14 / 2 = Radius (cm)
… oder noch einfacher:
Höhenunterschied (cm) / Steigung (%) x 15,92 = Radius (cm)
Daraus ergibt sich ein notwendiger Radius von ca. 53,1 cm für unsere Steigungsstrecke mit 3,0% Steigung und einem Höhenunterschied von 10 cm im 360º-Wendel.
Aber, Moment mal! In unserer Rechnung fehlt ja etwas. Wir haben die Steigungszugabe aufgrund der Steigung in einer Kurve noch nicht mit einkalkuliert. Nach der Formel 82 / Radius (cm) = Steigungszugabe (%) weiter oben beträgt die Steigungszugabe etwa 1,55 % und damit die scheinbare Steigung 4,55%, also viel zu viel für die meisten Züge und Lokomotiven.
Wenn wir den Höhenunterschied von Gleis zu Gleis nicht verringern wollen oder können, bleibt uns nur eine Lösung. Wir müssen die Steigungsstrecke und damit die tatsächliche Steigung verlängern. Das geht nur, indem wir den Radius der Steigungsstrecke vergrößern. Würden wir die Steigungszugabe von der maximal möglichen Steigung von 3% abziehen, verbleiben uns noch 1,45% für die tatsächlich mögliche Steigung. Daraus ergibt sich bei einem gewünschten Höhenunterschied von 10 cm eine Streckenlänge der Steigung von 10 cm / 1,45% x 100 = 689,6 cm und damit ein Radius von 689,6 cm / 3,14 / 2 = 109,8 cm. Bei diesem Radius hätten wir eine Steigungszugabe von 82 / 109,8 cm = 0,75% und wir kommen auf eine scheinbare Steigung von 2,25%. So kommen wir also nicht zu dem gewünschten Ergebnis. Der richtige Wert muss also irgendwo dazwischen liegen. Nur, wie finden wir ihn?
Wir kombinieren die obigen Formeln und stellen sie so um, dass sie folgendermaßen aussieht:
Nun setzen wir die Werte für den gewünschten Höhenunterschied (HU) und scheinbare Steigung (ST), also die, mit der die Lokomotive belastet werden darf, ein. Das Ergebnis nennt uns den Radius, den der Gleiswendel mindestens haben muss. Das Ergebnis wird uns wahrscheinlich überraschen, denn es ist meist größer, als wir geplant haben.
So ergibt die Formel bei einer gewünschten scheinbaren Steigung von 3% und einem Höhenunterschied von 10 cm einen Radius von mindestens 80,4 cm! Das ergibt sich aus folgender Rechnung: 10 (HU) x 15,92 ergibt 159,2. Zu dem Wert addieren wir 82, damit kommen wir auf 241,2. Das teilen wir durch 3,0 (ST) und erhalten den Wert 80,4 cm (R). Das sind also 27,3 cm mehr Radius, als die zu Beginn angenommenen 53,1 cm. Der Umfang des Gleiswendels einschließlich Gleiskörper wächst entsprechend von etwa 110 cm auf rund 165 cm an.
So einfach geht’s – den Lösungsweg zu finden, war nicht ganz so einfach.
Mein Dank geht an Bärbel, eine befreundete Mathematikerin und Ralf, ein befreundeter Physiker, die mir beim Um- und Zusammenbau der Formeln geholfen haben!
Wem die Anwendung der Formel zu kompliziert erscheint, findet in der unten stehenden Tabelle eine noch einfachere Hilfe. In der linken Spalte sucht man den gewünschten Höhenunterschied für einen 360º Gleiswendel und findet in den Spalten rechts daneben den benötigten Mindestradius für die gewünschte Steigung.
| Gewünschte Steigung | |||||
| Gewünschter Höhenunterschied | 1,5 % | 2 % | 2,5 % | 3 % | 3,5 % |
| 7 cm | 129,0 cm | 96,7 cm | 77,4 cm | 64,5 cm | 55,3 cm |
| 8 cm | 139,6 cm | 104,7 cm | 83,7 cm | 69,8 cm | 59,8 cm |
| 9 cm | 150,2 cm | 112,6 cm | 90,1 cm | 75,1 cm | 64,4 cm |
| 10 cm | 160,8 cm | 120,6 cm | 96,5 cm | 80,4 cm | 68,9 cm |
| 11 cm | 171,4 cm | 128,6 cm | 102,8 cm | 85,7 cm | 73,5 cm |
| 12 cm | 182,0 cm | 136,5 cm | 109,2 cm | 91,0 cm | 78,0 cm |
| 13 cm | 192,6 cm | 144,5 cm | 115,6 cm | 96,3 cm | 82,6 cm |
| 14 cm | 203,3 cm | 152,4 cm | 122 cm | 101,6 cm | 87,1 cm |
| 15 cm | 213,9 cm | 160,4 cm | 128,3 cm | 106,9 cm | 91,7 cm |
Einfacher geht’s nun wirklich nicht! Viel Spaß beim „Wendeln”!
- ✅ KOMPLETTES SET: Enthält alle benötigten Ständer, Fahrbahnsegmente und eine ausführliche Aufbauanleitung.
- ✅ VIELSEITIG VERWENDBAR: Ideal für Märklin, Trix, Fleischmann, Roco und Piko mit H0 Gleiswenden.
- ✅ SICHERE FAHRT: Außenkurven um 3 mm überhöht für erhöhte Fahrsicherheit.
- ✅ SPIRALAUFBAU: Ermöglicht das Überbrücken von Höhenunterschieden in Ihrer Modellbahnlandschaft.
- ✅ IDEAL FÜR MODELLBAU: Präzise gefertigte Holzbauteile für anspruchsvolle Modellbauer.
Hier gibt es Informationen zu den Modelleisenbahn-Radien in H0, die dafür in Frage kommen könnten.
Letzte Aktualisierung am 2.07.2025 / Affiliate Links / Bilder von der Amazon Product Advertising API
